Immersed manifold
It is a manifold $M$ together with a differentiable map
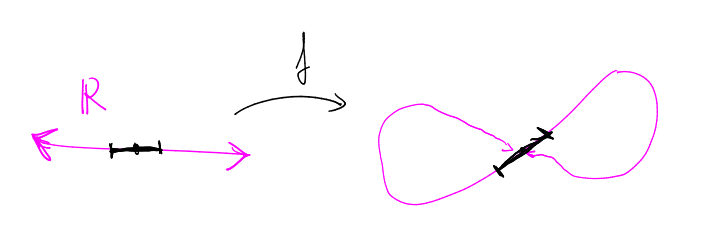
$$ f: M\longrightarrow \mathbb{R}^n $$satisfying $df(X)\neq 0$ iff $X\neq 0$ (and therefore it is a local diffeomorphism). It is also said that $f$ is an immersion.
It is a weaker notion that embedded manifold.
This notion can be generalized to any codomain $N$ (also a smooth manifold) instead of $\mathbb{R}^n$. It is verified the canonical immersion theorem.
On the other hand, an immersed manifold does not necessarily give rise to a submanifold. We have to require that $f$ be injective. An immersed submanifold would be a subset $M$ of $\mathbb R^n$ such that it is a immersed manifold with the identity map. The differentiable structure of $M$, and in particular, its topology, has nothing to do with that of $\mathbb{R}^n$.
Theorem (local embedding theorem). Given an immersion $f: M\longrightarrow N$ and a point $p\in M$ there exists a neighbourhood $V$ of $M$ such that the restriction $f|_{V}$ is an embedding.
$\blacksquare$
See @lee2013smooth Theorem 4.25
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: